
Calculations
Quantification of oligonucleotides
The quantity of an oligonucleotide usually is given as its total optical density (OD value), as amount of substance (nmol) or as its available mass (µg). The OD value is measured experimentally, then the other values are calculated.
Yield
OD value
The OD value of a sample at a wavelength of 260 nm is defined as the extinction that occurs in measuring absorption of the sample in 1 ml aqueous solution in a 1 cm cuvette at the respective wavelength. In practice, OD values are often outside of the linear measurement range of an UV spectrometer; therefore diluted samples have to be quantified and to be extrapolated to the total OD value.
Example:
The dried oligonucleotide is dissolved in 400 µl of sterile water. From this stock solution an aliquot of 10 µl is taken and filled up with sterile water to 1 ml. Now the extinction value of this diluted solution is measured in a photometer in a 1 cm quartz cuvette at a wavelength of 260 nm. The obtained extinction (e.g. 0,25) is multiplied with the aliquotation factor (400 µl/ 10 µl = 40). The result is the OD value (10 in our example).
Amount of oligonucleotide in nmol
According to the law of Lambert and Beer (E = Epsilon Ɛ * C * d) one can convert from the extinction E (OD value) to the concentration C and therefore to the amount of substance of the oligonucleotide. Strictly speaking, the extinction coefficient Epsilon Ɛ is different for each oligonucleotide sequence and would have to be ascertained empirically. In a good approximation it corresponds to the sum of the extinction coefficients of the individual nucleotides and the modifications in the sequence.
Using the oligo´s sequence data and the OD value one can calculate the amount of material as follows:
 |
E(260nm): OD-value n [nmol]: Amount in nmol
A,G,C,T: Number of the respective bases in the oligonucleotide
Epsilon Ɛ: Extinction coefficient of attached modifications
|
For mixed sequences the following values for the amount of material (nmol) result depending on oligo length:
| OD value | Oligo length [number of nucleotides] |
|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 1 | 9,4 | 4,7 | 3,1 | 2,3 | 1,9 | 1,6 | 1,3 | 1,2 | 1,0 | 0,9 |
| 3 | 28 | 14 | 9 | 7 | 5,6 | 4,7 | 4,0 | 3,5 | 3,1 | 2,8 |
| 10 | 94 | 47 | 31 | 23 | 19 | 16 | 13 | 12 | 10 | 9 |
| 25 | 234 | 117 | 78 | 59 | 47 | 39 | 33 | 29 | 26 | 23 |
| 100 | 937 | 468 | 312 | 234 | 187 | 156 | 134 | 117 | 104 | 94 |
For a rough estimate applies for a mixed 20mer oligonucleotide:
1 OD approximates 5 nmol (5000 pmol).
Amount of oligonucleotide in µg
Using the amount of substance in nmol and the oligo's molecular weight, one can calculate the amount of oligonucleotide in µg:
 |
n [µg]: Amount in µg n [nmol]: Amount in nmol
MW: Molecular mass
|
|
Also, for a mixed 20mer oligonucleotide roughly estimates: 1 OD approximates 30 µg DNA oligonucleotide |
Calculating concentrations
1. Concentration adjustment to x pmol/µl
A dried oligonucleotide is to be dissolved to obtain a concentration "c" of x pmol/µl.
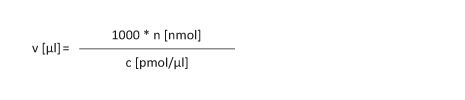 |
n [nmol]: Amount of substance in nmol c [pmol/µl]: Concentration
v [µl]: Volume of the oligos
|
Example:
An oligonucleotide (23 nmol) is to be dissolved with a target concentration of 50 pmol/µl in the resulting solution:
v [µl] = 1000 * 23 nmol / 50 pmol/µl = 460 µl
Remark:
The following concentrations are identical:
c [ pmol / µl ] = c [ nmol / ml ] = c [ µmol / l ] = c [ µM ]
Example: 248 pmol/µl = 248 nmol/ml = 248 µmol/l = 248 µM
2. Concentration when dissolving in a defined volume
A dried oligonucleotide is to be dissolved in a defined volume of water. Which concentration results?
 |
n [nmol]: Amount of substance in nmol c [pmol/µl]: Concentration
v [µl]: Volume of the oligos
|
|
Example: c[pmol/µl] = 1000 * 54 nmol / 200 µl = 270 pmol/µl |
Calculation of the molecular weight
The molecular weight of an oligonucleotide is calculated from the number of individual nucleotides in the oligonucleotide and from possible modifications of the oligonucleotide:
MWoligo (DNA) = 313,2*A + 329,2*G + 289,2*C + 304,2*T + MWmod - 62 [g/mol]
MWoligo (RNA) = 329,2*A + 345,2*G + 305,2*C + 306,2*U + MWmod - 62 [g/mol]
A,G,C,T: Number of bases in the DNA oligo
A,G,C,U: Number of bases in the RNA oligo
MWmod: Molecular weight of a modification, if present
Example:
5’- CCA GGC AGT CTT ATT TTG ACT-3’
MW = 313,2 * 4 + 329,2 * 4 + 289,2 * 5 + 304,2 * 8 – 62 = 6387,2 g/mol
Melting temperature
Melting temperature Tm
The melting temperature Tm of a DNA double strand is defined as the temperature at which 50% of the double strand have been denatured, thus being present in single stranded form. Length of the oligo, base composition and concentration of an oligonucleotide as well as the salt concentration in the solution have a key influences on the Tm value. There are different more or less exact methods of predicting the melting temperature:
a) Wallace Rule (2 + 4 Rule)1
This rule which is valid for very short oligonucleotides (up to about 15 bases) assumes a contribution of 2 °C for each AT-pair and of 4°C for each GC-pair to the melting temperature of a double strand:
Tm = 2°C * (A+T) + 4°C * (G+C)
b) Calculation by GC-content
The following formula based on Howly et al.2,3 takes mostly into account the GC content of the oligo and is valid for long oligonucleotides:
Tm = 81,5 + 0,41 (%GC) + 16,6 log c(M+) – 500/n –0,61 (%F) –1,2 D
with:
%GC = Percentage of GC-pairs
c(M+) = Concentration of mono-valent cations
n = Number of nucleotides
%F = Percentage of formamide in the buffer
D = Percentage of mismatches
c) Nearest Neighbor Method
The so-called Nearest-Neighbor-Method also takes into account sequence-dependent stacking effects for Tm calculation and is based on thermodynamic properties of neighbouring nucleotide pairs. This method is reliable for oligonucleotides of medium length (20 – 60 bases).
Formula:4
Tm = [(1000 *dH) /(A + dS + R * ln (C/4))] – 273.15 + 16,6 * log c(K+)
with:
H = Sum of the enthalpies of all pairs
dS = Sum of the entropies of all pairs
A = -10.8 cal, Entropy of helix formation
R = 1.984 cal/grad x mol, Gas constant
C = Oligonucleotide concentration (250 pmol/l)
c(K+) = Concentration of potassic ions in the oligo solution (50 mmol/l)
Thermodynamic data:5,6
| Dinucleotide | Enthalpy dH (kcal) | Entropy dS (cal) |
|---|---|---|
| AA | -9.1 | -24.0 |
| AG | -7.8 | -20.8 |
| AC | -6.5 | -17.3 |
| AT | -8.6 | -23.9 |
| GA | -5.6 | -13.5 |
| GG | -11.0 | -26.6 |
| GC | -11.1 | -26.7 |
| GT | -6.5 | -17.3 |
| CA | -5.8 | -12.9 |
| CG | -11.9 | -27.8 |
| CC | -11.0 | -26.6 |
| CT | -7.8 | -20.8 |
| TA | -6.0 | -16.9 |
| TG | -5.8 | -12.9 |
| TC | -5.6 | -13.5 |
| TT | -9.1 | -24.0 |
Example: 5'-GTC GAA CCG GAA ACC ACC CCT-3'
dH = -6.5 –5.6 –11.9 –5.6 –9.1 –6.5 –11.0 –11.9 –11.0 –5.6 –9.1 –9.1 – 6.5 –11.0 -5.8 -6.5 –11.0 –11.0 –11.0 –7.8 = -173.5
dS = -17.3 –13.5 –27.8 –13.5 –24.0 –17.3 –26.6 –27.8 –26.6 –13.5 –24.0 –24.0 –17.3 –26.6 –12.9 –17.3 -26.6 –26.6 –26.6 –20.8 = -430.6
Tm = (1000 x (–173.5))/ ((-10.8 –430.6 + 1.984 x ln (6.25 x 10-11)) – 273.15 + 16.6 log 50x10-3 = 60.7
All methods for the calculation of melting temperatures given above do not take into account modifications of the oligonucleotide (e.g. dyes, linkers).
Literature:
1. Wallace RB, Schaffer J, Murphy RF, Bonner J, Itakura K; Nuc. Acids Res. 1979, 6, 3543.
2. Howley PM, Israel MF, Law M-F, Martin MA; J. Biological Chemistry 1979, 254, 4876.
3. Teoule R, Bazin H, Fouqué B, Roget A, Sauvaigo S; Nucleosides & Nucleotides 1991, 10, 129.
4. Rychlik W, Spencer WJ, Rhoads RE; Nuc. Acids Res. 1990, 18, 6409-6413.
5. Breslauer KJ, Frank R, Blöcker H, Marky LA; Proc. Natl. Acad. Sci 1986, 83, 3736-3750.
6. Borer PN, Dengler B, Tinoco IJ, Uhlenbeck OC; J. Mol.Biol. 1983, 86, 843-853.

